Computable Performance Bounds on Sparse Recovery

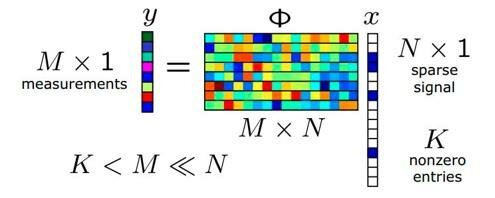
For my Advanced Image Processing course, I reproduced the work “Computable Performance Bounds on Sparse Recovery” (IEEE Transactions on Signal Processing, Vol. 63). The premise is that Compressive Sensing is very useful for collecting fewer measurements than the dimensionality of the output. However, existing theoretical bounds are primarily based on the Restricted Isometry Property. RIP is not easily verifiable for a given matrix, and the bounds obtained are very loose. The work introduces a novel bound whose necessary condition simulatenously

• is readily verifiable (linear number of convex optimizations)
• is easier to satisfy than the RIP bound (in expectation), and
• leads to tighter bounds than the RIP. The report and code for this work are available here.